Zitat:
[...]
Dazu ist es aber nötig, neben dem Erlernen von Fachbegriffen und
Rechenrezepten auch die Zusammenhänge und Hintergründe, die zu diesen
Algorithmen und Begriffen führen, zu verstehen.
- Dabei werden wiederum Kompetenzen und Strategien erworben, die auf andere Probleme übertragen werden können. Mathematik kann in diesem Sinne als „Gehirnjogging“ verstanden werden.
- Nicht zuletzt ist Mathematik genau aus diesem Grund die Sprache, derer sich die Naturwissenschaften (und auch manche Geisteswissenschaften) bedienen, um sich auszudrücken und gehört daher einfach zu unserem Kulturgut.
Schließlich will der
Mathematikunterricht am Gymnasium aber über den Utilitarismus hinaus die
Ästhetik und Schönheit des Fachs vermitteln.
- Mathematik kann durch überraschende Einsichten und „Aha-Effekte“ offene und vorurteilsfreie Gemüter begeistern.
[...]
entnommen aus:
mathematik.rwth-aachen.de
Zitat:
Im Vorkurs Mathematik wird eine Zusammenfassung wesentlicher Inhalte des
Schulstoffes vermittelt mit dem Ziel, den Übergang von der Schule zur
Hochschule sowohl fachlich als auch methodisch zu erleichtern.
- Sämtliche Themen werden hierbei unabhängig von den jeweiligen Vorkenntnissen neu entwickelt.
- (Notiz: ... "unabhängig von den jeweiligen Vorkenntnissen" ist nicht ganz korrekt ... es wird am Anfang schon Rücksicht von den "Lehrenden" genommen, aber es gibt unter den Studenten einige, die den Stoff beherrschen und während der Vorlesungen rücksichtslos laut sind und den Unterricht nachhaltig stören ... die sollte der Dozent ohne Berücksichtigung ihrer Kenntnisse aus dem Vorlesungssaal rausschmeißen ... zumal nach einigen Tagen durch den Stoff gerast wird und fast jeder plötzlich erkennt: der Abitursstoff ist aufgebraucht => die "Höhere Mathematik" steht lächelnd vor der Tür ... und selbst die lässt sich noch steigern für die "mathelastigen" Königsfächer "Physik" und "Mathematik", erst dann folgen "Maschinenbau", "Elektrotechnik" und "Informatik" ...)
[...]
Inhalte
Grundlagen
Zitat:
Analysis
- Rationale und Reelle Zahlen
bettermarks.com
Zitat:
Ich habe nie verstanden, was das Ergebnis von
zwölf Jahren Mathematikunterricht gewesen sein soll.
(Stefan Rogal)

matheguru.com
Zitat:
Ich habe nie verstanden, was das Ergebnis von
zwölf Jahren Mathematikunterricht gewesen sein soll.
(Stefan Rogal)
matheguru.com
- Anordnung, Absolutbetrag
- Ungleichungen
- Potenzrechnung mit ganzzahligen und rationalen Exponenten
- Aussagenlogik
- Mengenlehre
- Abbildungen (Funktion)
Zitat:
... eigentlich ist es ja keine Funktion,
da mehrere y-Werte auf einen x-Wert fallen ...
- Komplexe Zahlen
- Beweisverfahren der Mathematik
(Notiz: ... spätestens ab der Beweisführung scheiden sich die Geister => für viele endet schon in der schulischen Laufbahn ab diesem Punkt das Verständnis und die Sympathie für die Höhere Mathematik, da die Beweisführung so gar nicht nach einem echten Beweis klingt, sondern eher nach einer Fortführung und Erklärung eines Axioms (!), also die nähere, fachspezifische Erläuterung einer festgelegten (!) Wahrheit und Methode ... darüberhinaus scheint auch die Sprache manchmal im Widerspruch zur "Reinen Mathematik" zu stehen => so klingen Begriffe und Formulierungen wie "ein-eindeutig" oder "wir nehmen an" oder "wir setzen voraus" sehr spekulativ und willkürlich ...)
- Infimum & Supremum
- Elementare Funktionen
- Stetigkeit
" Die Reine Mathematik ist eindeutig ...
... die geschriebene und gesprochene
Mathematik ist es nicht !"
- Differentialrechnung
- Integralrechnung
- Matrixbegriff
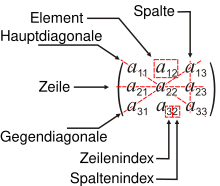
Zitat:
In der Mathematik versteht man unter einer Matrix (Plural Matrizen) eine rechteckige Anordnung (Tabelle) von Elementen meist mathematischer Objekte,
etwa Zahlen.
- Mit diesen Objekten lässt sich dann in bestimmter Weise rechnen, indem man Matrizen addiert oder miteinander multipliziert.
- Matrizen können beliebige Dimensionalität besitzen.
- Sie stellen Zusammenhänge, in denen Linearkombinationen eine Rolle spielen, übersichtlich dar und erleichtern damit Rechen- und Gedankenvorgänge.
Sie werden insbesondere dazu benutzt, lineare Abbildungen darzustellen und lineare Gleichungssysteme zu beschreiben und zu lösen.
[...]
- Lineare Gleichungsysteme
Zitat:
Das graphische Lösungsverfahren ist nur bei
Rechnerische Lösung mit 3 Unbekannten (x,y,z)
- Lineare Abhängigkeit
hier: zweidimensionaler Raum
schule-bw.de
Zitat:
Zitat:
Mit Vektoren lassen sich geometrische Zusammenhänge elegant beweisen.
- Beispielsweise lässt sich die Definition der linearen Unabhängigkeit von Vektoren ausnutzen.
Das Verfahren wird hier für Beweise der ebenen Geometrie beschrieben.
- Es funktioniert aber auch in analoger Weise im dreidimensionalen Raum.
- Analytische Geometrie

schule-studium.de//Schnittpunkt-Ebene-Koordinatenachsen

learnattack.de//abipruefung/originalpruefung
* * * *
(... Mathe in Abstufungen für
- Kindergarten
- Grundschule
- Mittelstufe
- Oberstufe
- Kaufmännische & naturwisschenschaftlich-technische Berufe
- Ingenieure & Programmierer
- Mathematiker & Physiker
Zitat:
[...]
Der OMB+ hat das Ziel, die Mathematikkenntnisse der Schule aufzufrischen und die notwendige Sicherheit beim Umgang mit mathematischen Konzepten und bei der Anwendung grundlegender Verfahren zu vermitteln.
Der OMB+ besteht aus erklärenden Texten mit vielen
- Beispielen,
- interaktiven Bildern,
- Übungsaufgaben
und
- Tests
an denen Sie ihr Können
selbst prüfen können.
- Alle Begriffe sind in dem Kurs erklärt.
- Sie benötigen keine zusätzlichen Hilfsmittel.
- Sie arbeiten wann, wo und wie oft Sie wollen.
- Sie benötigen nur einen Internetanschluss mit einem Standard-Browser.
- (Notiz: + Stift und Papier)
[...]
Ab jetzt gilt ein Schlussprüfung als bestanden, falls mindestens 80% der Punkte erreicht wurden.
Kurs:
Eingangstest MINT-Fit
Syntax
Syntax
- Komma = .
- Multiplikation = *
- Division = /
- Potenz = ^
- Wurzel = sqrt (...)
- Logarithmus zur Basis 10 bzw dekadischer Logarithmus = lg (...)
- Pi = pi
- 7/13 ist das Vierfache einer Zahl x. Um welche Zahl handelt es sich? Geben Sie Ihr Ergebnis als gewöhnlichen Bruch ein.
- Ein Betrag in Höhe von 10.000 Euro wird zu einem jährlichen Zinssatz von Euro wird zu einem jährlichen Zinssatz von 2% unter Berücksichtigung von Zinseszinsen für Jahre angelegt. Welche Summe steht dem Anleger nach Ablauf dieser 2 Jahre zur Verfügu
[...]
I Elementares Rechnen
II Gleichung in eine Unbekannten
III Ungleichung in einer Variablen
IV Lineare Gleichungssysteme
V Geometrie
VI Elementare Funktionen
VII Differenzialrechnung
VIII Integralrechnung
IX 2D Koordinatensystem
X Vektorgeometrie
* * * *
... für alle Bereiche gilt: der Erfolg kommt über das "Abstraktionsvermögen", "Fleiß" und "die Qualität der Lehre".
Da aber die "Lehre in den Schulen" teilweise grottenschlecht ist
Schön zu sehen in Quiz- und Wissenssendungen: sobald die Kandidaten einfache Rechenaufgaben gestellt bekommen, sieht man die Nervosität und Unsicherheit wachsen: ganz selten, dass einer von ihnen souverän eine Matheaufgabe löst => das ist ein typisches Beispiel dafür, dass der jahrelange Matheunterricht vergeudete Zeit ist, wenn nicht mal das Kopfrechnen gestärkt wird, ganz zu schweigen vom Fehlen, die Mathematik für jeden spielerisch schmackhaft zu machen ...)
Da aber die "Lehre in den Schulen" teilweise grottenschlecht ist
- - keine Anpassung der Lehr- und Lernmethoden an das geistige Fassungsvermögen und die individuelle Lerndynamik
- - Dominanz des Frontalunterrichts
Schön zu sehen in Quiz- und Wissenssendungen: sobald die Kandidaten einfache Rechenaufgaben gestellt bekommen, sieht man die Nervosität und Unsicherheit wachsen: ganz selten, dass einer von ihnen souverän eine Matheaufgabe löst => das ist ein typisches Beispiel dafür, dass der jahrelange Matheunterricht vergeudete Zeit ist, wenn nicht mal das Kopfrechnen gestärkt wird, ganz zu schweigen vom Fehlen, die Mathematik für jeden spielerisch schmackhaft zu machen ...)
* * * *